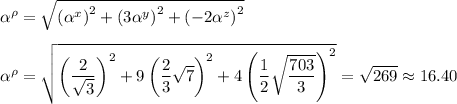2: For a sample of data
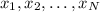 , the mean of this sample denoted by
, the mean of this sample denoted by
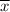 is the sum of the data divided by the number of data points,
is the sum of the data divided by the number of data points,
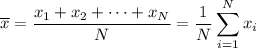
As an example, consider
 ,
,
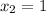 , and
, and
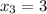 . Then
. Then
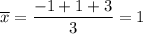
3: Standard deviation is a measure of how dispersed a given data sample is relative to the mean. Consult the plot: for a normal distribution, approximately 68% of it lies within 1 standard deviation of the mean, approx. 95% within 2 standard deviations, and approx. 99.7% within 3 standard deviations.
For instance, if the data is pulled from a normally distributed population with mean 0 and standard deviation 1, if you were to randomly select any data from the population, then 68% of the time it will fall in the range (-1, 1); 95% of the time it will fall within (-2, 2); 99.7% of the time it fall within (-3, 3).
To compute the standard deviation for a sample, for each
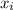 in
in
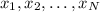 , you
, you
• take the difference between
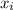 and the mean
and the mean
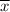
• square this difference
• sum all the squared differences
• divide the sum by N - 1 (for a sample) or N (for a population)
• take the square root
Here the standard deviation is denoted
 , which I would read as "the sample standard deviation of the data x" - sample because of the N - 1 subscript.
, which I would read as "the sample standard deviation of the data x" - sample because of the N - 1 subscript.
Continuing with the previous example, we'd have
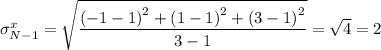
4: Not much more to say here, the standard error is basically a measure of how accurate a given estimate is about the population based on the sample data. It's analogous to uncertainty in measuring length with a ruler, for instance.
In our example,
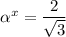
5: If x, y, and z are random variables, then I suppose ρ is meant to denote a function of these random variables (so that ρ itself is just another random variable). For instance, you could have ρ = x + 3y - 2z. Then
 is the sample mean of ρ.
is the sample mean of ρ.
I'm not entirely sure about the notation
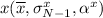 , but I suspect it's just referring to sample x with mean
, but I suspect it's just referring to sample x with mean
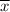 and standard deviation
and standard deviation
 with standard error
with standard error
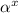 .
.
∆ρ is just the differential of ρ, essentially capturing how ρ changes with respect to small changes in x, y, and z. The expression you see here follows from the chain rule for differentiation.
The formula you see for
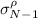 is the sample standard deviation of ρ. Think of ∆ρ as a vector with 3 components. Then
is the sample standard deviation of ρ. Think of ∆ρ as a vector with 3 components. Then
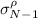 is the magnitude of this vector.
is the magnitude of this vector.
Similarly,
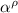 is the standard error for ρ, and corresponds to the magnitude of the vector whose components are the standard errors of x, y, and z.
is the standard error for ρ, and corresponds to the magnitude of the vector whose components are the standard errors of x, y, and z.
In order for these statistics to make sense, each of x, y, and z must be samples of the same number of data. Say we take x as before
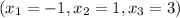 , along with
, along with
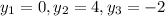 and
and
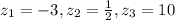 . Suppose ρ = x + 3y - 2z. Then
. Suppose ρ = x + 3y - 2z. Then
• the sample means of y and z :
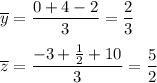
• the standard deviations of y and z :
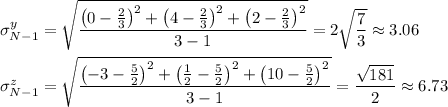
• the values of ρ :
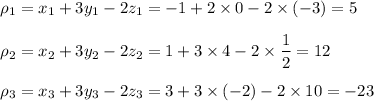
• the sample mean of ρ :
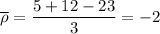
• by the chain rule,
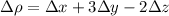
so the standard deviation of ρ :
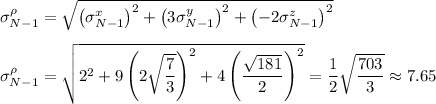
• the standard errors of y and z :

• the standard error of ρ :