Answer:
0.0143 = 1.43% probability that first 4 digits of the code are even numbers.
Explanation:
Arrangements of n elements:
The number of possible arrangements of n elements is given by:
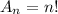
Probability:
A probability is the number of desired outcomes divided by the number of total outcomes.
In this question:
Desired outcomes:
First four digits are even(2, 4, 6 and 8 are even, so arrangements of 4 elements).
Last four digits are odd(1, 3, 5 and 7 are odd, so the last four elements are also arrangements of 4 elements). So
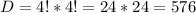
Total outcomes:
Arrangements of 8 digits. So
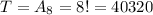
Probability:
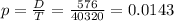
0.0143 = 1.43% probability that first 4 digits of the code are even numbers.