Question

Determine the diameter of wire with a circular cross-section that has tensile force of 60.0Newtons, and this force produces a stress of 3 060 000 pascal ​

Answer 1

the diameter of the wire is 5 mm.

Step-by-step explanation:

Given;

tensile force of the wire, F = 60 N

stress on the wire, δ = 3,060,000 Pa = 3,060,000 N/m²

Let A be the cross sectional area of the wire

The cross sectional area of the wire is calculated as follows;

`\sigma = (F)/(A) \\\\A = (F)/(\sigma) \\\\A = (60)/(3,060,000) = 1.961 * 10^(-5) \ m^2`

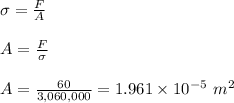
The diameter of the wire is calculated as follows;

`A = (\pi d^2)/(4) \\\\d = \sqrt{(4A)/(\pi) } \\\\d = \sqrt{(4* 1.961 * 10^(-5))/(\pi) } \\\\d = 5.0 * 10^(-3) \ m\\\\d = 5 \ mm`

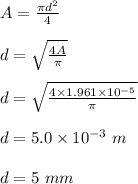
Therefore, the diameter of the wire is 5 mm.