Question

In a gas equation, (P+a/v²)(v-b)=RT... What are the dimensions of a ​

Answer 1

The dimensions of a is L⁵·M·T⁻²mol⁻²

Step-by-step explanation:

The gas equation for a real gas, can be presented as follows;

`\left (P + (n^2 \cdot a)/(V^2) \right) \cdot \left (V - n \cdot b\right) = R \cdot T`

Where;

P = The pressure

V = The volume

a = A constant representing intermolecular forces

b = A constant representing molecular volume

n = The number of moles

The dimensions of the expression
`P + (n^2 \cdot a)/(V^2)` is in units of pressure, given that 'P' is in units of pressure, bar, therefore, the expression,
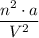`(n^2 \cdot a)/(V^2)`, is also measured in units of pressure

The dimensions of pressure, P = M·L⁻¹·T⁻²

'n²' unit dimension is mol², while V² is measured as liter² (L³), therefore, 'a' will convert the units of n² and V² to bars, therefore, we have;

The unit dimension of a = L²·bar/(mol²)

(L³)²·(M/(L·T²))/(mol²) = L⁵·M·T⁻²mol⁻²

The dimension of a = L⁵·M·T⁻²mol⁻²

Where;

L = Length in meters

T = Time in seconds

M = Mass in kilogram