Answer:
We expect 17.82, that is, approximately 18 people to be universal donors.
Explanation:
For each person, there are only two possible outcomes. Either they are universal donors, or they are not. The probability of a person being an universal donor is independent of any other person. This means that we use the binomial probability distribution to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
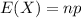
The standard deviation of the binomial distribution is:

Only about 6.6% of the American population has O-negative blood.
This means that
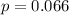
If 270 unrelated people give blood in a certain week, how many of these people do we expect to be universal donors?
This is E(X) when
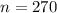 . So
. So
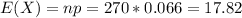
We expect 17.82, that is, approximately 18 people to be universal donors.