Question

I don't understand what I did wrong, please help​

Answer 1

`(3)/(16) x^(3)-(9)/(4)x+6 = y`

Explanation:

Lets start with the easiest part of this question - simply plugging in to get easier equations:

`-8a+4b-2c+d=9\\`

`8a+4b+2c+d=3`

Something that now immedietly pops out is that many of the terms would cancel if we added them together. We get the following results by adding the two equations together:

`8b+2d = 12`

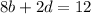
Now lets look at the other bit of inromation the question gives you -- that the two points are horizontal tangents. Taking the derivative of the standard form of a cubic, we get:

`y' = 3ax^2+2bx+c`

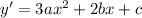
Since the points are both horizontal tangents, y' will be equal to 0 at the points. Thus, plugging in we get:

`y'(-2) = 0 = 12a-4b+c`

`y'(2) = 0 = 12a+4b+c`

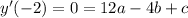
We again see a simple subtracting opportunity that will cancel out two terms:

`-8b = 0`

`b = 0`

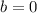
Now going back to the equation we got by adding the two equations that we got from simply plugging our points in:

`d = 6`

Now that we have b and d, we can now plug them back into our step one and derivative equations in order to get a simple system:

`-8a - 2c=3`

`12a+c=0`

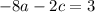
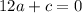
Solving for a and c, we get:

`a = (3)/(16)`

`c = (-9)/(4)`

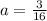
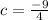
Thus, finally, our answer is:

`(3)/(16) x^(3)-(9)/(4)x+6 = y`

Attached is desmos, which you can use to check.