Question

Calculus (yet again)!

The water level of a certain body of water is changing at a rate of
`W(t) = (1)/(2)cos(3 - (t)/(2))` inches per hour, where t represents hours since 12 a.m.
What is the average hourly number of inches that the water level changes for this lake in one day?

I'm pretty sure that the number of inches that the water changes in one day would be represented by
`\int\limits^2_0 {W(t)} \, dt` (where the number on top of the integral is a 24), but how would I set up an integral for the average hourly number of inches? Thank you so much!

Answer 1

The average hourly number of inches that the water level changes per day is about 0.0231 inches per hour.

Explanation:

The water level of a certain body of water is changing at a rate represented by the function:

`\displaystyle W(t) = (1)/(2)\cos \left( 3- (t)/(2)\right)`

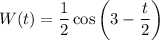
Where W is measured in inches per hour and t represents hours since 12 A.M.

And we want to determine the average hourly number of inches that the water level changes for the lake in one day.

Recall that the average value of a function is given by:

`\displaystyle f_\text{avg} = (1)/(b-a) \int_(a)^(b) f(x) \, dx`

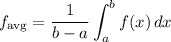
Hence, the find the average hourly number of inches that the water level changes in one day, we simply need to find the average value of W from t = 0 to t = 24.

Substitute:

`\displaystyle W(t)_{\text{avg}} = (1)/((24)-(0)) \int_(0)^(24) (1)/(2)\cos \left(3 - (t)/(2)\right) \, dt`

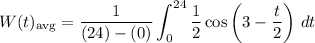
Simplify:

`\displaystyle W(t)_{\text{avg}} = (1)/(24) \int_(0)^(24) (1)/(2)\cos \left(3 - (t)/(2)\right) \, dt`

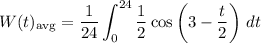
Evaluate using u-substitution. We can let:

`\displaystyle u = 3 - (t)/(2) \Rightarrow du = -(1)/(2)\, dt\Rightarrow -2\, du = dt`

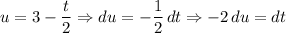
Hence:

`\displaystyle W(t)_{\text{avg}} = -(1)/(24) \int_(3)^(-9) \cos u \, du`

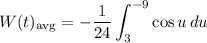
Evaluate:

`\displaystyle \begin{aligned} W(t)_{\text{avg}} &= (1)/(24)\int_(-9)^(3) \cos u\, du \\ \\ &= (1)/(24)\left(\sin u\Big|_(-9)^(3)\right) \\ \\ &= (1)/(24)\left(\sin3 - \sin -9\right) \\ \\ &=(1)/(24)\left(\sin 3 + \sin 9\right) \\ \\ &\approx0.0231 \end{aligned}`

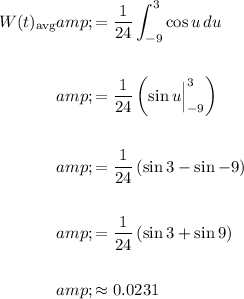
In conclusion, the average hourly number of inches that the water level changes per day is about 0.0231 inches per hour.