Question

Geometry: find the value of x. Round to the nearest tenth. How do I do this? screenshot attached

Answer 1

`\boxed {\boxed {\sf x \approx 105.3}}`

Explanation:

To solve for x, remember the right triangle trigonometry ratios (soh-cah-toa).

• sinθ= opposite/hypotenuse
• cosθ= adjacent/hypotenuse
• tanθ= opposite/adjacent

If we look at the angle given (θ), then we see that 36 is adjacent or next to the 70° angle. x is the hypotenuse because it is opposite the right angle. So, we have to use cosine (adjacent and hypotenuse).

`cos (\theta)=\frac {adjacent}{hypotenuse}`

`cos(70)=(36)/(x)`

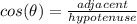
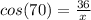
Cross multiply. (Multiply the first numerator by the second denominator. Then, multiply the first denominator by the second numerator).

`(cos(70))/(1)=(36)/(x)`

`cos(70)*x= 36`

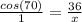
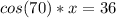
Since we want to solve for x, we must isolate the variable. Divide both sides by the cosine of 70.

`(cos(70)*x)/(cos(70))=( 36)/(cos(70))\\x= 105.2569584`

Round to the nearest tenth. The 5 in the hundredth place tells us to round the 2 to a 3.

`x \approx 105.3`

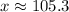
x is about 105.3