Question

Find the distance between the points (-6, – 7) and (5. – 7).

Answer 1

11

Explanation:

d=√(5-(-6))²+(-7-(-7))²

d=√(11²+0²)

d=11

Answer 2

`\boxed {\boxed {\sf d= 11}}`

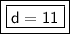
Explanation:

We are asked to find the distance between 2 points. We will use the distance formula.

`d= \sqrt{ (x_2-x_1)^2+(y_2-y_1)^2`

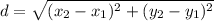
In this formula, (x₁ , y₁) and (x₂ , y₂) are the points. We are given the points (-6, -7) and (5, -7). If we match the value and the corresponding variable, we see that:

• x₁ = -6
• y₁ = -7
• x₂ = 5
• y₂ = -7

Substitute these values into the formula.

`d= \sqrt{(5- -6)^2 + (-7--7)^2`

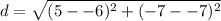
Solve inside the parentheses. Remember that two back-to-back negative signs become a plus sign.

• (5 - - 6) = (5 +6) = 11
• ( -7 - - 7) = (-7 +7) = 0

`d= \sqrt{ (11)^2+(0)^2`

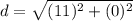
Solve the exponents.

• (11)² = 11 * 11 = 121
• (0)² = 0*0= 0

`d= \sqrt{(121)+(0)`

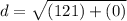
Add.

`d= √(121)`

`d=11`

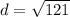
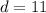
The distance between (-6, -7) and (5, -7) is 11.