Question

Asian Treats makes dumplings and spring rolls in batches. The two main ingredients for these items are meat and spiced starch. There are 25 pounds of meat and 16 pounds of spiced starch. To make a batch of dumplings, you need 5 pounds of meat and 2 pounds of spiced starch. The spring rolls need 5 pounds of meat and 4 pounds of spiced starch. The demand for dumplings is consistent at 5 batches. The store makes a profit of $1 per batch of dumplings and $5 for a batch of spring rolls. Determine the number of batches of dumplings and spring rolls to produce each day so that profit will be maximized. Solve this model by using graphical analysis. (You have to show your solutions using the graphical method) Make sure to shade the feasible region AND provide your optimal answers. How much flour and spiced starch will be left unused if Asian Treats makes the optimal batch

Answer 1

Let Asian treats makes
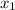`$x_1$` number of dumplings and
`$x_2$` number of spring rolls to maximize the profit.

Meat Spice starch

Dumplings 5 2

Spring rolls 5 4

Since there are 25 pounds of meat and 16 pounds of spice starch.

Therefore,
`$5x_1 + 5x_2 \leq 25$`

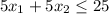
and
`$25x_1 + 4x_2 \leq 16$`

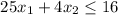
So profit per batch is

`$z= x_1 + 5x_2$`

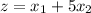
Therefore, the LPP is

Maximize
`$z= x_1 + 5x_2$`

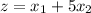
subject to the constraints

`$x_1+x_2 \leq 5$`

`$x_1+2x_2 \leq 8$` ,
`$x_1,x_2 \geq 0$`

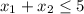
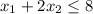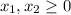
From the graph, the feasible region is OAPD

z at 0,
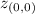`$z_((0,0))$` = 0

z at A,
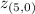`$z_((5,0))$` = 5 + 5(0)

= 5

z at P,
`$z_((2,3))$` = 2 + 5(3)

= 17

z at D,
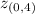`$z_((0,4))$` = 0 + 5(4)

= 20

Therefore, the maximum profit at D i.e. when
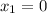`$x_1 = 0$` and
`$x_2 = 4$`.

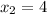So Asian Treats makes 0 dumpling and 4 spring rolls per latch to maximize the profit, and the profit is $ 20 per latch.

To produce 4 spring roll, Asian Treat needs 4 x 5 = 20 pound meat and 4 x 4 = 16 pound spice starch.

∴ The unused meat = 25 - 20

= 5 pounds