Question

Find all the cube roots of -8+8i(sqrt)3

Answer 1

Explanation:

We need to find cube roots of

`- 8 + 8i √(3)`

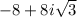
Let put this into trig form.

`r( \cos(x) + i \: sin(x)`

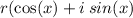
To find the radius we do this formula,

`r = \sqrt{ {a}^(2) + {b}^(2) }`

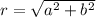
where a is the real number and b is the coeffeicent of the imaginary term.

`r = \sqrt{ - 8 {}^(2) + (8 √(3) ) {}^(2) } = √(64 + 192) = √(256) = 16`

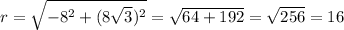
So our r value 16.

We need to find x, so we do this rule.

`\tan(x) = (b)/(a)`

`\tan(x) = - √(3)`

`(x) = (2\pi)/(3)`

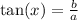
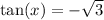
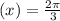
So our x is

`x = (2\pi)/(3)`

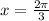
Now, we can simply our trig form,

`16 ( \cos( (2\pi)/(3) ) + \sin( (2\pi)/(3) ) )`

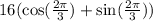
Now, we must find the cube roots of this.

This what we do,

Step 1: Take the cube root of 16., which is

`2 \sqrt[3]{2}`

Step 2: Divide the x values, which 2pi/3 by 3.

So now we get

`( (2\pi)/(3) )/(3) = (2\pi)/(9)`

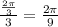
Step 3: Divide 2 pi by 3 and add that 2 times to 2pi/9.

`(2\pi)/(9) + (2\pi)/(3) + (2\pi)/(3) = (14\pi)/(9)`

So our cube root of this is

`2 \sqrt[3]{2} ( \cos (14\pi)/(9) + i \: sin \: (14\pi)/(9) )`