The question is incomplete. The complete question is :
A common "rule of thumb" for many reactions around room temperature is that the rate will double for each ten degree increase in temperature. Does the reaction you have studied seem to obey this rule? (Hint: Use your activation energy to calculate the ratio of rate constants at 300 and 310 Kelvin.)
Solutions :
If we consider the activation energy to be constant for the increase in 10 K temperature. (i.e. 300 K → 310 K), then the rate of the reaction will increase. This happens because of the change in the rate constant that leads to the change in overall rate of reaction.
Let's take :
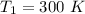
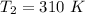
The rate constant =
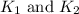 respectively.
respectively.
The activation energy and the Arhenius factor is same.
So by the arhenius equation,
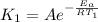 and
and
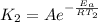
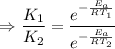
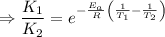
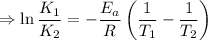
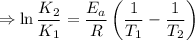
Given,
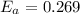 J/mol
J/mol
R = 8.314 J/mol/K
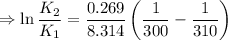
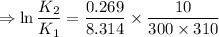
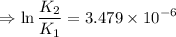
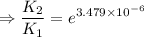
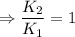
∴
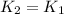
So, no this reaction does not seem to follow the thumb rule as its activation energy is very low.