Question

In a physics lab experiment, a compressed spring launches a 24 g metal ball at a 35o angle above the horizontal. Compressing the spring 17cm causes the ball to hit the floor 2.0 m below the point at which it leaves the spring after traveling 5.3 m horizontally. What is the spring constant

Answer 1

k = 45.95 N/m

Step-by-step explanation:

First, we will find the launch speed of the ball by using the formula for the horizontal range of the projectile.

`R = (v_(o)^(2)\ Sin\ 2\theta)/(g) \\\\v_(o)^(2) = (Rg)/(Sin\ 2\theta)\\`

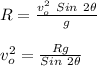
where,

Vo = Launch Speed = ?

R = Horizontal Range = 5.3 m

θ = Launch Angle = 35°

Therefore,

`v_(o)^(2) = ((5.3\ m)(9.81\ m/s^(2)))/(Sin\ 2(35^(o)))\\`

v₀² = 55.33 m²/s²

Now, we know that the kinetic energy gain of ball is equal to the potential energy stored by spring:

`Kinetic\ Energy\ Gained\ By\ Ball = Elastic\ Potential\ Energy\ Stored\ in \ Spring\\(1)/(2)mv_(o)^(2) = (1)/(2)kx^(2)\\\\k = (mv_(o)^(2))/(x^2) \\`

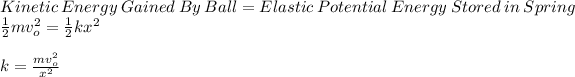
where,

k = spring constant = ?

x = compression = 17 cm = 0.17 m

m = mass of ball = 24 g = 0.024 kg

Therefore,

`k = ((0.024\ kg)(55.33\ m^2/s^2))/((0.17\ m)^2) \\`

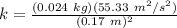
k = 45.95 N/m