Answer:
The z-score is 3.03.
Explanation:
The null hypothesis is:
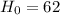
The alternate hypotesis is:
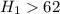
The z-score is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
Spencer sampled 50 students of a private school who were questioned about their scores in Mathematics.
This means that

Spencer wants to test the hypothesis that the private school students score better than the general public which has an average of 62 marks with a population standard deviation of 7 marks.
This means that
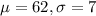
If the sample mean is 65 marks, what is the z-score
This is z when
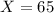 . So
. So

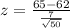
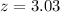
The z-score is 3.03.