Solution :
Time (sec) Volume of NaOH (mL)
339 26.23
1242 27.80
2745 29.70
4546 3.81
 39.81
39.81
Now the example of the first order kinetics w.r.t volumetric analysis is :
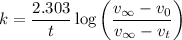
Here,
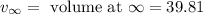
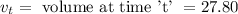
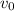 = volume at time 0 = 0
= volume at time 0 = 0
Since the interval is not constant, we take the time interval as
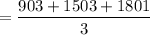
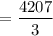
= 1402.3333
≈ 1402 seconds
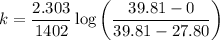
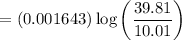
= 0.001643 x 0.52045
= 0.00082
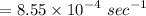
Therefore, the first order rate constant is k
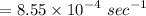 .
.