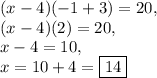Answer:
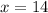
Explanation:
If two values are inversely proportional, their product must be maintained. That way, if one value goes up, the other goes down by the same extent.
Therefore, if
 and
and
 vary inversely, their product will be the same for all values of
vary inversely, their product will be the same for all values of
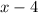 and
and
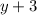 .
.
Let
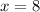 and
and
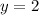 as given in the problem. Substitute values:
as given in the problem. Substitute values:
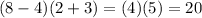
Hence, the maintained product is
 .
.
Thus, we have the following equation:
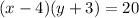
Substitute
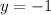 to find the value of
to find the value of
 when
when
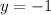 :
: