Answer:
a)
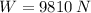
b)
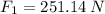
c)
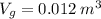
Step-by-step explanation:
a)
El peso del cuerpo es:
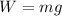
g es la gravedad (9.81 m/s²)
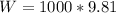
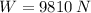
b)
Usando el principio de Pascal tenemos:
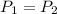
y la presion es la fuerza sobre el area.
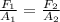
- F(1) es la fuerza aplicada en el embolo pequeño
- A(1) es el area del disco pequeño
- F(2) es la fuerza aplicada en el embolo grande
- A(2) es el area del disco grande
Despejando F(1):
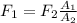
el area del plato es:
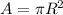
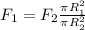
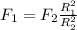
F(2) es el peso del cuerpo de 1000 kg (W)
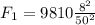
Por lo tanto, la fuerza que se debe hacer es:
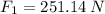
c)
Como tenemos un sistema cerrado el volumen de agua que desciende por el embolo pequeño debe ser igual al que sube por el grande, por lo tanto:
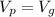
Vp es el volumen de agua en el émbolo pequeño
Vg es el volumen de agua en el émbolo grande
Como sabemos que son cilindros (V=πR²h)
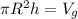
Entonces el volumen del émbolo mayor será:
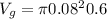
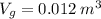
Espero te haya sido de ayuda!