Answer:
he times are getting closer as we use each filter, in the expression n would be the number of filters
t =
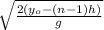
Step-by-step explanation:
For this exercise let's use the kinematics relations
y = y₀ + v₀ t - ½ g t²
When the first filter reaches the ground, its height is y = 0, as they release its initial velocity is zero
for the 1st filter
0 = y₀ - ½ g t²
t² = 2y₀ / g
t =
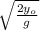
when we release the second filter upon arrival it has a height y = h where h is the height of each filter
h = y₀ - ½ g t²
t =
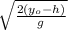
when we release the third filter it reaches y = 2h
2h = y₀ - ½ g t²
t =
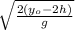
we can write the terms of this succession
(n-1) = y₀ -
 g t²
g t²
t =
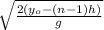
therefore we see that the times are getting closer as we use each filter, in the expression n would be the number of filters