Answer:
(a)
vf_1s = 5.19 m/s
h_1s = 10.095 m
vf_4s = 24.23 m/s
h_4s = 4.49 m (below railing)
(b)
vi = 9.9 m/s
(c)
t = 1.53 s
h = 34.41 m
Step-by-step explanation:
(c)
First, we will use the 1st equation of motion to find the time to attain the highest point:
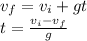
where,
t = time to attain maximum height = ?
vf = final velocity = 0 m/s (ball momentarily stops at highest point
vi = initial velocity = 15 m/s
g = - 9.81 m/s (for upward motion)
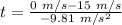
t = 1.53 s
Now, for the height attained we will use the 2nd equation of motion:
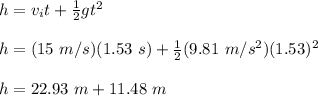
h = 34.41 m
(b)
using the 3rd equation of motion for a height of 5 m:
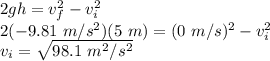
vi = 9.9 m/s
(c)
At t = 1 s:
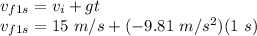
vf_1s = 5.19 m/s
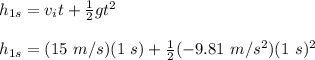
h_1s = 10.095 m
At t = 4 s:
Since the ball covers the maximum height of 34.41 m in 1.53 s and then starts moving downward.
Therefore for the remaining 4 s - 1.53 s = 2.47 s, the initial velocity will be 0 m/s at the highest point and the value of g will be positive due to downward motion.
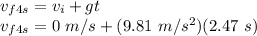
vf_4s = 24.23 m/s
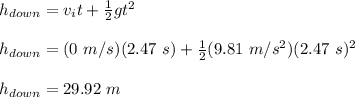
now, for the position with respect to railing:
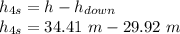
h_4s = 4.49 m (below railing)