Hi! I'm happy to help!
To solve this, we need to simplify all of the equations. There are 3 ways equations like this can go, infinitely many solutions, 1 solution, or no solution. Infinitely many is something like 6=6, that could mean infinite solutions because 6 always equal 6, and would apply in infinitely many ways. (in the equation) One solution refers to something like x=6. This tells your exactly what x is, and that is your only solution. (for the equation) And no solution is something like 5=6, 5 will never equal 6, so that is no solution. (to the equation)
Now, let's start out with our first equation. To find if our equations have solutions or not, we need to simplify them. We do this by singling out x to see what the solution is (if there is one).
x-9=2(x-3)+12
We can multiply 2, by x and -3 inside of the parenthesis, to simplify:
x-9=2x-6+12
Since we have at least one x on both sides, we can subtract it to isolate it:
x-9=2x-6+12
-x -x
-9=x-6+12
Combine -6 and twelve:
-9=x-6+12
-9=x+6
Now, we subtract 6 to fully isolate x:
-9=x+6
-6 -6
-15=x
We see we have 1 solution, so you should not pick option 1.
Second equation:
5(-2x + 7) + 3 = -10x + 38
We should first multiply the parenthesis:
-10x+35+3=-10x+38
Since we want to simplify, let's add 10x on both sides
-10x+35+3=-10x+38
+10 +10x
35+3=38
Add 35 and 3:
38=38
Since 38 will always equal 38, there are infinite solutions, and you should not pick option 2.
Third equation:
(6x - 4) = 3(x - 2)
Since there is nothing outside of the parenthesis (right side), we don't need them:
6x-4=3(x-2)
From here, multiply the parenthesis:
6x-4=3x-6
Subtract 3x from both sides:
6x-4=3x-6
-3x -3x
3x-4=-6
Add 4 to both sides to isolate x:
3x=-2
Divide both sides by 3, to fully isolate x:
x=-
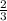
Since there is only 1 solution, you should not pick option 3.
Fourth equation: (not sure if the 100 is supposed to be there)
0.01x + 0.001 = (x + 10)
First, let's subtract 0.01x from both sides:
0.001=9.99x+10
Then, we subtract 10 from both sides to start isolating x:
-9.999=9.99x
Then, we divide both sides by 9.99:
______
1.000900900=x
Kind of a weird number, but regardless, you should not pick option 4, because it has 1 solution.
Fifth equation:
3(x + 2) + 1 = x + 2(4 + x)
First, let's multiply the parenthesis on both sides:
3x+6+1=x+8+2x
Combine like terms:
3x+7=3x+8
Subtract 3x from both sides:
7=8
7 will never equal 8, there will be no solution, and you should pick option 5.
You should pick option e, because it has no solution.
I hope this was helpful, keep learning! :D