Answer:
![\displaystyle (d)/(dx)[\sec x] = \sec x \tan x](https://img.qammunity.org/2022/formulas/mathematics/college/9veecjam7zc6liv93ehvucogr9obdn5bqp.png)
General Formulas and Concepts:
Pre-Calculus
Calculus
Differentiation
- Derivatives
- Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Quotient Rule]:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2022/formulas/mathematics/high-school/hrfl3gpx3dh352g7a9uj6guyxz9uxwhvl3.png)
Explanation:
*Note:
This is a known trigonometric derivative.
Step 1: Define
Identify
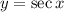
Step 2: Differentiate
- Rewrite [Trigonometric Identities]:
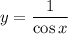
- Derivative Rule [Quotient Rule]:
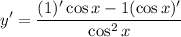
- Basic Power Rule:
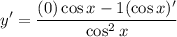
- Trigonometric Differentiation:
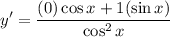
- Simplify:
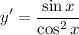
- Rewrite:
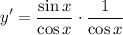
- Rewrite [Trigonometric Identities]:

Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation