Question

Show that 6 – 4x - x^2 can never be greater than 10.
( This is an Additional Math Question )

Answer 1

see explanation

Explanation:

Given

6 - 4x - x²

Since the coefficient of the x² term < 0 then parabola has a maximum vertex.

To find the x- coordinate of the vertex

`x_(vertex)` = -
`(b)/(2a)`

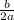
with a = - 1 and b = - 4 , then

`x_(vertex)` = -
`(-4)/(-2)` = - 2

The corresponding y- coordinate is found by substituting x = - 2 , that is

6 - 4(- 2) - (- 2)² = 6 + 8 - 4 = 10

vertex = (- 2, 10 )

The maximum value of the function is the y- coordinate of the vertex

Then maximum value is 10

Thus 6 - 4x - x² is never greater than 10