Question

Olivia likes to eat both apples and bananas. At the grocery store, each apple costs $0.20 and each banana cost $0.25. Olivia’s utility function for apples and bananas is given by U(A, B) = 6√AB where MUA = 3√B/A and MUB = 3√A/B . If Olivia has $4 to spend on apples and bananas, how many of each should she buy to maximize her satisfaction? [In the exam, you should be able to calculate MUa and MUb by yourself!] You may also try using the Lagrange optimization method to solve this question.

Answer 1

Therefore, Olivia should buy 10 apples and 8 bananas to maximize her utility.

Step-by-step explanation:

Let A represent the number of apples bought and B represent the number of bananas bought. Therefore since Olivia has $4 to spend:

0.2A + 0.25B = 4 (1)

Also, the tangency condition can be used to find the optimal amount of A to relative to B. It is give as:

`MU_A/P_A=MU_B/P_B\\\\\frac{3\sqrt{(B)/(A) } }{0.2}= \frac{3\sqrt{(A)/(B) } }{0.25}\\\\15\sqrt{(B)/(A) }=12\sqrt{(A)/(B) }\\\\squaring\ both\ sides:\\\\(225B)/(A) =(144A)/(B)\\\\225B^2=144A^2\\\\B^2=0.64A^2\\\\Taking\ square\ root:\\\\B=0.8A`

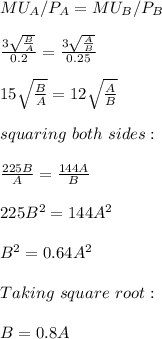
Put B = 0.8A in equation 1:

0.2A + 0.25(0.8A) = 4

0.2A + 0.2A = 4

0.4A = 4

A = 10

B = 0.8(A) = 0.8(10) = 8

Therefore, Olivia should buy 10 apples and 8 bananas to maximize her utility.