Question

Calculus please help

Answer 1

The balloon is rising at a rate of 50π/3 feet per minute.

Explanation:

A weather balloon is rising vertically while being observed from a point who is exactly 300 feet away from the spot directly beneath the ground.

This is represented in the diagram below.

We want to find the rate at which the balloon is rising (i.e. find dh/dt) when the angle between the ground and the observer is π/6 (i.e. when θ = π/6), and is increasing at a rate of π/24 radians per minute (i.e. when dθ/dt = π/24).

Write a ratio relating the variables:

`\displaystyle \tan \theta = (h)/(300)`

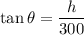
Take the derivative of both sides with respect to t:

`\displaystyle (d)/(dt)\left[ \tan\theta\right] = (d)/(dt)\left[ (h)/(300)\right]`

Implicitly Differentiate:

`\displaystyle \sec^2\theta \cdot (d\theta)/(dt) = (1)/(300) (dh)/(dt)`

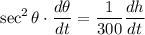
Substitute in known values:

`\displaystyle \sec^2 \left((\pi)/(6)\right) \left((\pi)/(24)\right) = (1)/(300) (dh)/(dt)`

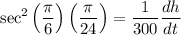
Solve for dh/dt:

`\displaystyle \begin{aligned} (dh)/(dt) &= 300\left(\sec^2\left((\pi)/(6)\right)\left((\pi)/(24)\right)\right) \\ \\ &= 300\left((4)/(3)\right)\left((\pi)/(24)\right) \\ \\ &= (50\pi)/(3) \text{ feet per minute}\end{aligned}`

In conclusion, the balloon is rising at a rate of 50π/3 feet per minute.