Question

The parallel plates in a capacitor, with a plate area of 9.30 cm2 and an air-filled separation of 4.50 mm, are charged by a 7.80 V battery. They are then disconnected from the battery and pulled apart (without discharge) to a separation of 9.60 mm. Neglecting fringing, find (a) the potential difference between the plates, (b) the initial stored energy, (c) the final stored energy, and (d) the work required to separate the plates.

Answer 1

a) ΔV ’= 1.66 10¹ V= 16.6 V, b) U = 55.64 10⁻¹² J, c) U_f = 1.18 10⁻¹⁰ J

d) W = 6.236 10⁻¹¹ J

Step-by-step explanation:

Capacitance can be found for a parallel plate capacitor

C = ε₀
`(A)/(d)`

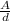
Let's reduce the magnitudes to the SI system

A = 9.30 cm² (1 m / 10² cm) 2 = 9.30 10⁻⁴ m²

c = 4.50 mm (1 m / 1000 mm) = 4.50 10⁻³ m

Co = 8.85 10⁻¹² 9.30 10⁻⁴ /4.50 10⁻³

Co = 1.829 10⁻¹² F

when the plates separate at d = 9.60 10⁻³ m, the capcitance changes to

C = ε₀ \frac{A}{d_1}

C = 8.85 10⁻¹² 9.30 10⁻⁴/9.60 10⁻³

C = 8.57 10⁻¹³ F

a) the potential difference

C =

since the capacitor is not discharged, let's look for the initial charge

Co = \frac{Q}{ \Delta V}

Q = C₀ ΔV

Q = 1.829 10⁻¹² 7.80

Q = 14.2662 10⁻¹² C

when the condensate plates are separated

C = \frac{Q}{ \Delta V' }

ΔV ’= Q / C

ΔV ’= 14.266 10⁻¹² / 8.57 10⁻¹³

ΔV ’= 1.66 10¹ V= 16.6 V

b) the stored energy is

U = ½ C ΔV²

for initial separation

U = ½ C₀ ΔV²

U = ½ 1.829 10⁻¹² 7.80²

U = 55.64 10⁻¹² J

c) The energy for end separation;

U_f = ½ C DV’2

U_f = ½ 8.57 10⁻¹³ 16,6²2

U_f = 1.18 10⁻¹⁰ J

d) The work

as there are no losses, the work is equal to the variation of the energy

W = ΔU = U_f -U₀

W = 1.18 10⁻¹⁰ - 55.64 10-12

W = 6.236 10⁻¹¹ J