Answer:
6, 21, and 23 inches
Explanation:
The perimeter of a triangle is equal to the sum of all side lengths in that triangle. We're given the perimeter as 50 inches, and the side lengths as n, 3n + 3, and 2n + 11.
- This means that we can algebraically solve the equation
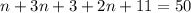
Step 1: Combine like terms.
Step 2: Subtract 14 from both sides.
Step 3: Divide both sides by 6.
Step 4: Plug in the value of n as 6 in each side.
Therefore, the side lengths are 6, 21, and 23 inches.
Have a lovely rest of your day/night, and good luck with your assignments! ♡