Question

2) X and Y are jointly continuous with joint pdf

Answer 1

From what I gather from your latest comments, the PDF is given to be

`f_(X,Y)(x,y)=\begin{cases}cxy&\text{for }0\le x,y \le1\\0&\text{otherwise}\end{cases}`

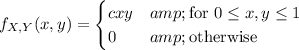
and in particular, f(x, y) = cxy over the unit square [0, 1]², meaning for 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1. (As opposed to the unbounded domain, x ≤ 0 *and* y ≤ 1.)

(a) Find c such that f is a proper density function. This would require

`\displaystyle\int_0^1\int_0^1 cxy\,\mathrm dx\,\mathrm dy=c\left(\int_0^1x\,\mathrm dx\right)\left(\int_0^1y\,\mathrm dy\right)=\frac c{2^2}=1\implies \boxed{c=4}`

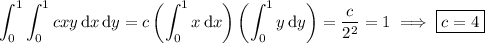
(b) Get the marginal density of X by integrating the joint density with respect to y :

`f_X(x)=\displaystyle\int_0^1 4xy\,\mathrm dy=(2xy^2)\bigg|_(y=0)^(y=1)=\begin{cases}2x&\text{for }0\le x\le 1\\0&\text{otherwise}\end{cases}`

(c) Get the marginal density of Y by integrating with respect to x instead:

`f_Y(y)=\displaystyle\int_0^14xy\,\mathrm dx=\begin{cases}2y&\text{for }0\le y\le1\\0&\text{otherwise}\end{cases}`

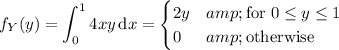
(d) The conditional distribution of X given Y can obtained by dividing the joint density by the marginal density of Y (which follows directly from the definition of conditional probability):

`f_(X\mid Y)(x\mid y)=(f_(X,Y)(x,y))/(f_Y(y))=\begin{cases}2x&\text{for }0\le x\le 1\\0&\text{otherwise}\end{cases}`

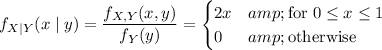
(e) From the definition of expectation:

`E[X]=\displaystyle\int_0^1\int_0^1 x\,f_(X,Y)(x,y)\,\mathrm dx\,\mathrm dy=4\left(\int_0^1x^2\,\mathrm dx\right)\left(\int_0^1y\,\mathrm dy\right)=\boxed{\frac23}`

`E[Y]=\displaystyle\int_0^1\int_0^1 y\,f_(X,Y)(x,y)\,\mathrm dx\,\mathrm dy=4\left(\int_0^1x\,\mathrm dx\right)\left(\int_0^1y^2\,\mathrm dy\right)=\boxed{\frac23}`

`E[XY]=\displaystyle\int_0^1\int_0^1xy\,f_(X,Y)(x,y)\,\mathrm dx\,\mathrm dy=4\left(\int_0^1x^2\,\mathrm dx\right)\left(\int_0^1y^2\,\mathrm dy\right)=\boxed{\frac49}`

(f) Note that the density of X | Y in part (d) identical to the marginal density of X found in (b), so yes, X and Y are indeed independent.

The result in (e) agrees with this conclusion, since E[XY] = E[X] E[Y] (but keep in mind that this is a property of independent random variables; equality alone does not imply independence.)