Question

Pleaseeeeeeeeeee help.

Remy stands on a dock at the edge of a lake represented by point C. Points A and B represent two buoys anchored in the lake. Remy plans to swim from C to A, then to B, and then back to C. The shortest distance from Remy to the swim route AB¯¯¯¯¯¯¯¯ is 60 meters and is measured from C to D.

Answer 1

The total distance Remy will swim is approximately 236 meters

Explanation:

From the given diagram, of triangle ΔCAB, we have that the path Remy is to swim are;

1) Length of segment C to A

2) Length of segment A to B

3) Length of segment B to C

The length of the perpendicular at point D on segment AB to C = 60 meters

Therefore, DC = 60 m

By trigonometric ratios, we have;

`tan (\theta) = (Opposite \ leg \ length)/(Adjacent \ leg \ length)`

`cos(\theta) = (Adjacent\ leg \ length)/(Hypotenuse \ length)`

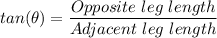
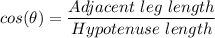
We are given the values of the trigonometric ratios of the following angles;

tan(27°) = 0.51

tan(43°) = 0.93

cos(27°) = 0.89

cos(43°) = 0.73

∴ tan(43°) = AD/DC = 0.93

Where the lengths of AC, AD, DB, DC and BC

AD = DC × tan(43°)

∴ AD = 60 × 0.93 ≈ 55.8

Similarly, we have;

tan(27°) = DB/DC

∴ DB = DC × tan(27°)

DB = 60 × 0.51 ≈ 30.6

From
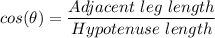`cos(\theta) = (Adjacent\ leg \ length)/(Hypotenuse \ length)`, we have;

cos(43°) = DC/AC

AC = DC/(cos(43°))

∴ AC = 60/0.73 ≈ 82.2

Similarly, we have;

cos(27°) = DC/BC

BC = DC/(cos(27°))

∴ BC = 60/0.89 ≈ 67.4

The total distance Remy will swim = AC + AD + DB + BC

∴ The total distance Remy will swim = 82.2 + 55.8 + 30.6 + 67.4 = 236

The total distance Remy will swim = 236 meters