Question

Assume that each time a metal detector at an airport signals, there is a 25% chance that the cause is change in the passenger's pocket. During a given hour, 15 passengers are stopped because of a signal from the metal detector. a) Find the probability that at least 3 passengers will have been stopped due to change in their pockets. b) If 15 passengers are stopped by the detector, would it be unusual for none of these to have been stopped due to change in the pocket

Answer 1

a) 0.7639 = 76.39% probability that at least 3 passengers will have been stopped due to change in their pockets.

b) 0 is less than 2.5 standard deviations from the mean, so it would not be unusual.

Explanation:

For each passenger, there are only two possible outcomes. Either they will have been stopped due to a change in the pocket, or not. Passengers are independent. This means that we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
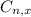`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

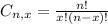
And p is the probability of X happening.

The expected value of the binomial distribution is:

`E(X) = np`

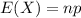
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

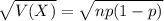
A measure is considered unusual if it is more than 2.5 standard deviations of the mean.

25% chance that the cause is change in the passenger's pocket.

This means that
`p = 0.25`

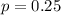
During a given hour, 15 passengers are stopped because of a signal from the metal detector.

This means that
`n = 15`

a) Find the probability that at least 3 passengers will have been stopped due to change in their pockets.

This is

`P(X \geq 3) = 1 - P(X < 3)`

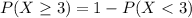
In which

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)`

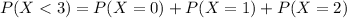
So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(15,0).(0.25)^(0).(0.75)^(15) = 0.0134`

`P(X = 1) = C_(15,1).(0.25)^(1).(0.75)^(14) = 0.0668`

`P(X = 2) = C_(15,2).(0.25)^(2).(0.75)^(13) = 0.1559`

`P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0134 + 0.0668 + 0.1559 = 0.2361`

`P(X \geq 3) = 1 - P(X < 3) = 1 - 0.2361 = 0.7639`

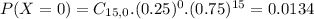
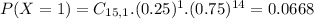
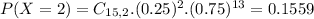
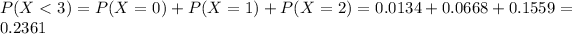
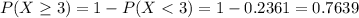
0.7639 = 76.39% probability that at least 3 passengers will have been stopped due to change in their pockets.

b) If 15 passengers are stopped by the detector, would it be unusual for none of these to have been stopped due to change in the pocket

First we find the mean and the standard deviation:

`E(X) = np = 15*0.25 = 3.75`

`√(V(X)) = √(np(1-p)) = √(15*0.25*0.75) = 1.68`

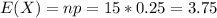
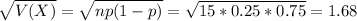
3.75 - 2.5*1.68 = -0.45

0 is less than 2.5 standard deviations from the mean, so it would not be unusual.