Question

24. The expression ax2 + bx + c takes the values 0, 1 and 4 when x takes the values 1, 2

and 3 respectively. Find the value of the expression when x takes the value 4.


Please solve it for me

Answer 1

When x takes the value of 4, the expression takes the value of 9.

Explanation:

We are given that the expression:

`\displaystyle ax^2 + bx + c`

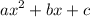
Evaluates to 0, 1, and 4 when x = 1, 2, and 3, respectively.

And we want to determine the value of the expression when x = 4.

The expression evaluates to 0 when x = 1. In other words:

`\displaystyle a(1)^2 + b(1) +c = a + b + c = 0`

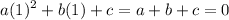
We can complete the same for the other two:

`\displaystyle a(2)^2 + b(2) + c = 4a + 2b + c = 1\text{ and } \\ \\ a(3)^2 + b(3) + c = 9a + 3b + c = 4`

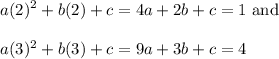
This yields a triple system of equations:

`\displaystyle \left\{ \begin{array}{l} a + b + c = 0 \\ 4a + 2b + c = 1 \\ 9a + 3b + c = 4 \end{array}`

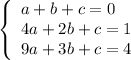
Solve. We can cancel out the c by multiplying the first equation by negative one and adding it to both the second and the third:

`\displaystyle \begin{aligned} (4a + 2b + c) + (-a - b -c ) &= (-0) + (1) \\ \\ 3a +b &= 1\end{aligned}`

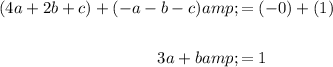
And:

`\displaystyle \begin{aligned} (9a + 3b + c) + (-a - b -c) &= (-0) + (4) \\ \\ 8a + 2b &= 4\end{aligned}`

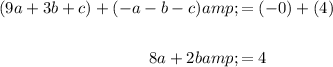
Solve for the two resulting equations. We can multiply the first by negative two and add it to the second:

`\displaystyle \begin{aligned}(8a + 2b) + (-6a -2b) &= (4) + (-2) \\ \\ 2a &= 2 \end{aligned}`

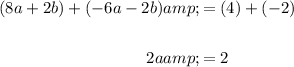
Hence:

`a = 1`

Solve for b:

`\displaystyle \begin{aligned} 3a + b &= 1 \\ b&= 1 - 3a \\ b&= 1 - 3(1) \\ b &= -2\end{aligned}`

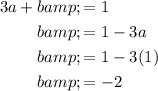
And finally, solve for c:

`\displaystyle \begin{aligned} a + b + c &= 0 \\ (1) + (-2) + c &= 0 \\ c &= 1\end{aligned}`

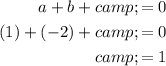
Hence, our expression is:

`\displaystyle x^2 -2x + 1`

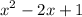
Then when x = 4:

`\displaystyle (4)^2 - 2(4) + 1= 9`

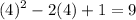
In conclusion, when x = 4, the resulting value is 9.