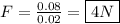Question

What was the final momentum?

what was the initial velocity of the 0.2 kg cart?
if the collision lasted 0.02 s, what force did each cart exert on the other?​

Answer 1

Hello!

Recall the equation for momentum:

`\huge\boxed{ p = mv}`

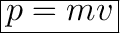
p = linear momentum (kgm/s)

m = mass (kg)

v = velocity (m/s)

Part 1:

We can solve for the total momentum using the above equation. Let m1 represent the 0.2 kg cart, and m2 represent the 0.4 kg cart.

`p = m_1v_1' + m_2v_2'`

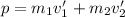
Since they move off together:

`p = v_f(m_1 + m_2) = 0.2(0.2 + 0.4) = \boxed{0.12 kg(m)/(s)}`

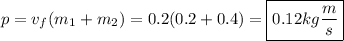
Part 2:

Using the conservation of momentum:

`m_1v_1 + m_2v_2 = m_1v_1' + m_2v_2'\\\\`

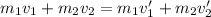
m2 was initially at rest, so:

`m_1v_1 + m_2(0) = 0.12\\\\0.2(v_1) = 0.12\\\\v_1 = (0.12)/(0.2) = \boxed{0.6 (m)/(s)}`

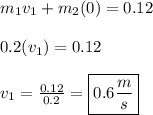
Part 3:

We can calculate the force by first calculating the impulse exerted on the carts.

Recall the equation for impulse:

`\large\boxed{I = m\Delta v = m(v_f - v_i}}`

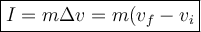
We can use either cart, but for ease, we can use the 0.4 cart that starts from rest.

Thus:

`I = 0.4(0.2 - 0) = 0.08 kg(m)/(s)`

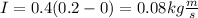
Now, calculate force with the following:

`\large\boxed{I = Ft, F = (I)/(t)}`

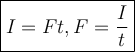
Plug in the values:

`F = (0.08)/(0.02) = \boxed{4 N}`