Answer:
v = ( 6.41 i^ + 8.43 j^ + 2.63 k^ ) m/s
Step-by-step explanation:
We can solve this problem using the kinematic relations, we have a three-dimensional movement, but we can work as three one-dimensional movements where the only parameter in common is time (a scalar).
X axis.
They indicate the initial position x = 8 m, its initial velocity v₀ = 5.5 m / s, the force Fx₁ = 220 N x₁ = 14 m, now the force changes to Fx₂ = 100 N up to the point xf = 17 m. The final speed is wondered.
As this movement is in three dimensions we must find the projection of the initial velocity in each axis, for this we can use trigonometry
the angle fi is with respect to the in z and the angle theta with respect to the x axis.
sin φ = z / r
Cos φ = r_p / r
z = r sin φ
r_p = r cos φ
the modulus of the vector r can be found with the Pythagorean theorem
r² = (x-x₀) ² + (y-y₀) ² + (z-z₀) ²
r² = (14-8) 2 + (-21 + 30) 2+ (-7 +4) 2
r = √126
r = 11.23 m
Let's find the angle with respect to the z axis (φfi)
φ = sin⁻¹ z / r
φ = sin⁻¹ (
 )
)
φ = 15.5º
Let's find the projection of the position vector (r_p)
r_p = r cos φ
r_p = 11.23 cos 15.5
r_p = 10.82 m
This vector is in the xy plane, so we can use trigonometry to find the angle with respect to the x axis.
cos θ = x / r_p
θ = cos⁻¹ x / r_p
θ = cos⁻¹ (
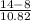 )
)
θ = 56.3º
taking the angles we can decompose the initial velocity.
sin φ = v_z / v₀
cos φ = v_p / v₀
v_z = v₀ sin φ
v_z = 5.5 sin 15.5 = 1.47 m / z
v_p = vo cos φ
v_p = 5.5 cos 15.5 = 5.30 m / s
cos θ = vₓ / v_p
sin θ = v_y / v_p
vₓ = v_p cos θ
v_y = v_p sin θ
vₓ = 5.30 cos 56.3 = 2.94 m / s
v_y = 5.30 sin 56.3 = 4.41 m / s
we already have the components of the initial velocity
v₀ = (2.94 i ^ + 4.41 j ^ + 1.47 k ^) m / s
let's find the acceleration on this axis (ax1) using Newton's second law
Fₓx = m aₓ₁
aₓ₁ = Fₓ / m
aₓ₁ = 220/100
aₓ₁ = 2.20 m / s²
Let's look for the velocity at the end of this interval (vx1)
Let's be careful if the initial velocity and they relate it has the same sense it must be added, but if the velocity and acceleration have the opposite direction it must be subtracted.
vₓ₁² = v₀ₓ² + 2 aₓ₁ (x₁-x₀)
let's calculate
vₓ₁² = 2.94² + 2 2.20 (14-8)
vₓ₁ = √35.04
vₓ₁ = 5.92 m / s
to the second interval
they relate it to xf
aₓ₂ = Fₓ₂ / m
aₓ₂ = 100/100
aₓ₂ = 1 m / s²
final speed
v_{xf}² = vₓ₁² + 2 aₓ₂ (x_f- x₁)
v_{xf}² = 5.92² + 2 1 (17-14)
v_{xf} =√41.05
v_{xf} = 6.41 m / s
We carry out the same calculation for each of the other axes.
Axis y
acceleration (a_{y1})
a_{y1} = F_y / m
a_{y1} = 460/100
a_[y1} = 4.60 m / s²
the velocity at the end of the interval (v_{y1})
v_{y1}² = v_{oy}² + 2 a_{y1{ (y₁ -y₀)
v_{y1}2 = 4.41² + 2 4.60 (-21 + 30)
v_{y1} = √102.25
v_{y1} = 10.11 m / s
second interval
acceleration (a_{y2})
a_{y2} = F_{y2} / m
a_{y2} = 260/100
a_{y2} = 2.60 m / s2
final speed
v_{yf}² = v_{y1}² + 2 a_{y2} (y₂ -y₁)
v_{yf}² = 10.11² + 2 2.60 (-27 + 21)
v_{yf} = √ 71.01
v_{yf} = 8.43 m / s
here there is an inconsistency in the problem if the body is at y₁ = -27m and passes the position y_f = -21 m with the relationship it must be contrary to the velocity
z axis
first interval, relate (a_{z1})
a_{z1} = F_{z1} / m
a_{z1} = -200/100
a_{z1} = -2 m / s
the negative sign indicates that the acceleration is the negative direction of the z axis
the speed at the end of the interval
v_{z1}² = v_{zo)² + 2 a_{z1} (z₁-z₀)
v_{z1}² = 1.47² + 2 (-2) (-7 + 4)
v_{z1} = √14.16
v_{z1} = -3.76 m / s
second interval, acceleration (a_{z2})
a_{z2} = F_{z2} / m
a_{z2} = 210/100
a_{z2} = 2.10 m / s2
final speed
v_{fz}² = v_{z1}² - 2 a_{z2} | z_f-z₁)
v_{fz}² = 3.14² - 2 2.10 (-3 + 7)
v_{fz} = √6.94
v_{fz} = 2.63 m / s
speed is v = ( 6.41 i^ + 8.43 j^ + 2.63 k^ ) m/s