Answer:
El ángulo formado entre las dos direcciones es aproximadamente 115º.
Explanation:
Las direcciones dadas en el enunciado significan lo siguiente:
S32ºE - 32º al este del sur.
E57ºN - 57º al norte del este.
Vectorialmente hablando, cada dirección es la siguiente:
S32ºE
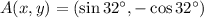
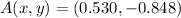
E57ºN
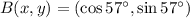
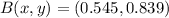
El ángulo formado entre los dos vectores unitarios (
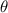 ), medido en grado sexagesimales, puede determinarse mediante la siguiente ecuación vectorial:
), medido en grado sexagesimales, puede determinarse mediante la siguiente ecuación vectorial:
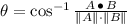
Donde:
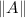 - Norma de
- Norma de
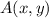 .
.
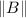 - Norma de
- Norma de
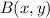 .
.
Si sabemos que
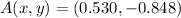 ,
,
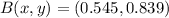 ,
,
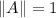 y
y
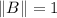 , entonces el ángulo formado entre los dos vectores es:
, entonces el ángulo formado entre los dos vectores es:
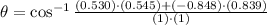
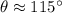
El ángulo formado entre las dos direcciones es aproximadamente 115º.