Question

you have to prepare a ph 5.03 buffer, and you have the following 0.10m solutions available: hcooh, hcoona, ch3cooh, ch3coona, hcn, and nacn. How many milliliters of each solution would you use to make approximately a liter of the buffer?

Answer 1

The buffer is the one that contains weak acid (the
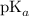`$\text{pK}_a$` is nearly equal to the required pH) and the salt of its conjugate base.

The
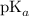`$\text{pK}_a$` values of the given weak acids are as follows :

HCOOH :
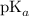`$\text{pK}_a$` = 3.744

`$CH_3COOH : pK_a = 4.756$`

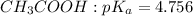
HCN :
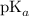`$\text{pK}_a$` = 9.21

Since the required pH is 5.03, the suitable buffer is the mixture of the acetic acid and the salt of its conjugate base.

Let suppose the volumes of
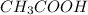`$CH_3COOH$` and
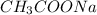`$CH_3COONa$` are x and y mL respectively.

So the total volume of the buffer is 1000 mL.

∴ x+ y = 1000 ................(1)

Writing the Henderson-Hasselbalch equation for the given buffer solution :

`$pH = pK_a + \log \ ([CH_3COONa])/([CH_3COOH])$` .............(2)

`$5.03 = 4.756 + \log \ (\left((y \ mL * 0.10 \ M)/((x+y) \ mL)\right))/(\left((x \ mL * 0.10 \ M)/((x+y) \ mL)\right))$`

`$5.03 = 4.756+ \log (y)/(x)$`

`$(y)/(x)=10^(5.03-4.756)$`

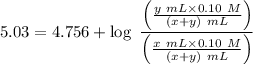
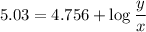
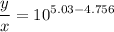
y = 1.9 x

Substituting the values of y in equation (1), we get

x + 1.9 x = 1000

x = 345

Putting the value of x in (1), we get

345 + y = 1000

y = 655

Therefore the volume of
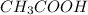`$CH_3COOH$` is 345 mL and the volume of
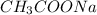`$CH_3COONa$` is 655 mL.