Question

Two consecutive positive multiples of 8 have a product of 2,688. What is the difference of these numbers?

Answer 1

8

Explanation:

Let one of the multiples of 8 be 8x and the second multiple of 8 be 8(x+1). Using x and x+1 ensure that the resulting multiples are one multiple apart, or consecutive. Next, recall that these two consecutive multiples of 8 have a product of 2,688. We can thus write the equation:

`8x*8(x+1)=2,688`.

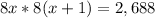To solve the equation, we must simplify and distribute. We can isolate the non-zero terms on one side the equation and solve the remaining quadratic equation for x:

`64x(x+1)-2688\\64^2+64x-2688=0\\54(x^2+x-42)=0\\64(x+7)(x-6)=0`

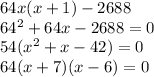
This means that x=-7 or x=6. Using the positive result x=6 gives the multiples of 8×6 and 8(6+1) or 48 and 56. Subtract the two numbers ot find the difference is 56-48 or 8.