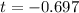Answer:
The t-test statistic is
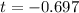
Explanation:
The test statistic is:
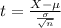
In which X is the sample mean,
 is the expected mean,
is the expected mean,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
The sample standard deviation is 7.309.
This means that
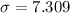
Adam reads that the average speed that cars drive on the highway is 65 mph.
This means that
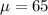
60.5, 63.2, 54.7, 51.6, 72.3, 70.7, 67.2, and 65.4 mph.
8 values, so

The sample mean is:
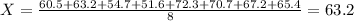
Test statistic:
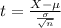
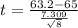
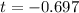
The t-test statistic is