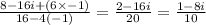Answer:
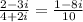
Explanation:
To simplify an expression like this, we multiply top and ottom of the fraction (denominator and numerator) by the complex conjugate of the bottom (numerator). For a complex expression (a+bi), the complex conjugate is (a−bi). When we do the calculation, it will become clear why this works so well.
Note that (a−bi)/(a−bi) is just the same as 1, so when we do this multiplication the result is the same number we started with.
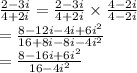
But
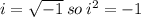
Using this and collecting like terms, we have: