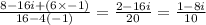Question

The expression 2-3i/4+2i
is equivalent to

Answer 1

`(2 - 3i)/(4 + 2i) = (1 - 8i)/(10)`

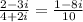
Explanation:

To simplify an expression like this, we multiply top and ottom of the fraction (denominator and numerator) by the complex conjugate of the bottom (numerator). For a complex expression (a+bi), the complex conjugate is (a−bi). When we do the calculation, it will become clear why this works so well.

Note that (a−bi)/(a−bi) is just the same as 1, so when we do this multiplication the result is the same number we started with.

`(2 - 3i)/(4 + 2i) = (2 - 3i)/(4 + 2i) * (4 - 2i)/(4 - 2i ) \\ = \frac{8 - 12i - 4i + 6 {i}^(2) }{16 + 8i - 8i - 4 {i}^(2) } \\ = \frac{8 - 16i + 6 {i}^(2) }{16 - 4 {i}^(2) }`

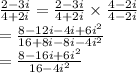
But

`i = √( - 1) \: so \: {i}^(2) = - 1`

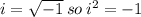
Using this and collecting like terms, we have:

`(8 - 16i + (6 * - 1) )/(16 - 4 ( - 1) ) = (2 - 16i)/(20) = (1 - 8i)/(10)`