Question

MADD (Mother's Against Drunk Drivers) wishes to estimate the proportion of adult drivers that have run at least one red light in the last month. A poll is conducted on a simple random sample of adult drivers and it is found that out of 1251 adult drivers, 641 of them have run at least one red light in the last month. You will be finding a 90% confidence interval for the fraction of adult drivers that run at least one red light in the last month.

Required:
Check that the normality assumptions are met?

Answer 1

Normality assumptions are met.

The 90% confidence interval for the proportion of adult drivers that run at least one red light in the last month is (0.4892, 0.5356).

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

A poll is conducted on a simple random sample of adult drivers and it is found that out of 1251 adult drivers, 641 of them have run at least one red light in the last month.

This means that
`n = 1251, \pi = (641)/(1251) = 0.5124`

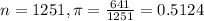
Normality assumptions:

We need that:
`n\pi \geq 10, n(1-\pi)\geq 10`

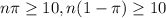
We have that:

`n\pi = 1251*0.5124 = 641`

`n(1-\pi) = 1261*0.4876 = 610`

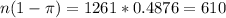
So normality assumptions are met.

90% confidence level

So
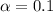`\alpha = 0.1`, z is the value of Z that has a pvalue of
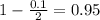`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

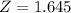The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.5124 - 1.645\sqrt{(0.5124*0.4876)/(1251)} = 0.4892`

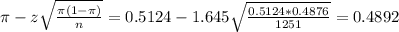
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.5124 + 1.645\sqrt{(0.5124*0.4876)/(1251)} = 0.5356`

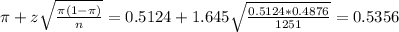
The 90% confidence interval for the proportion of adult drivers that run at least one red light in the last month is (0.4892, 0.5356).