Question

A bakery works out a demand function for its chocolate chip cookies and finds it to be q = D(x) = 760 - 13x​, where is the quantity of cookies sold when the price per​ cookie, in​ cents, is x.

A) Find the elasticity. ​
B) At what price is the elasticity of demand equal to​ 1?
C) At what prices is the elasticity of demand​ elastic?
A. Prices are elastic at all values.
B. Prices cannot be elastic in this case.
C. Greater than.
D. Less than .
D) At what prices is the elasticity of demand​ inelastic?
A. Greater than.
B. Less than.
C. Prices are inelastic at all values.
D. Prices cannot be inelastic in this case.
E) At what price is the revenue a​ maximum?
F) At a price of ​¢ per​ cookie, will a small increase in price cause the total revenue to increase or​ decrease?
A. Increase.
B. Decrease.

Answer 1

1. 13x/760-13x

2. X = 29.23

3. X> 29.23

4. X<29.23

5. Max price = 29.23c

Explanation:

1. D(x) = 760-13x

To get Elasticity, we differentiate the equation

D'x = -13

Elasticity is expressed as:

E(x) = -x*D'(x)/760-13x

= X(-13)/760-13x

`(-13x)/(760-13x)`

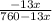
B. Price elasticity with demand = 1

13x/760-13x = 1

We cross multiply

13x = 1(760-13x)

13x = 760-13x

Collect like terms

26x = 760

X = 29.23

C. When elasticity of demand is elastic

13x/760-13x > 1

We cross multiply

13x > 1(760-13x)

13x > 760-13x

Collect like terms

26x > 760

X > 29.23

C. Greater than 29.23

D. When inelastic

This follows same solution as 2 and 3 but the sign is different.

E(x) <1

13x/760-13x < 1

We cross multiply

13x < 1(760-13x)

13x < 760-13x

Collect like terms

26x < 760

X < 29.23

B. less than 29.23

E. We get total revenue

X(760-13X)

= 760x - 13x²

We differentiate this

760-26x = 0

760 = 26x

X = 29.23

revenue is a maximum at price is 29.23c

f. The last question is incomplete