Question

The fence around Wayne Manor is going to be replaced. No fence will be required on the side lying along Gotham River. If the new wrought iron fence costs $12 per meter for the side parallel to the river, and $4 per meter for the other two sides, find the dimensions of the maximum area that can be enclosed by the fence if Bruce Wayne cannot spend more than $3600.

Answer 1

Explanation:

Let the side parallel to the river be x meter and the other two sides be of y meter, then

`12 x+(2 y)(4)=3600`

`12 x+8 y &=3600`

`3 x+2 y &=900`

`2 y &=900-3 x`

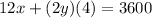
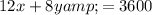
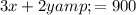
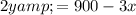
The area of the rectangle is
`A=xy`

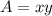
Substitute into to express the area in a single variable x as,

`A(x) &=x\left[(1)/(2)(900-3 x)\right]`

`=(1)/(2)\left(900 x-3 x^(2)\right)`

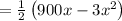
Differentiate A(x) with respect to x and equate to zero as,

`A^(\prime)(x) &=0`

`(d)/(d x)\left[(1)/(2)\left(900 x-3 x^(2)\right)\right]=0`

`900-3(2 x) =0`

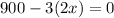
x=150

Here,
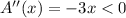`A^(\prime \prime)(x)=-3 x<0` at
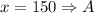`x=150 \Rightarrow A` is maximum

Therefore, the dimension is:

Length of side parallel to the river: x=150 m.

Length of other two side:
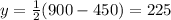`y=(1)/(2)(900-450)=225` m.