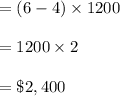Question

The city of Smallville is considering whether to build a new public swimming pool. This pool would have a capacity of 800 swimmers per day, and the proposed admission fee is $6 per swimmer per day. The estimated cost of the swimming pool, averaged over the life of the pool, is $4 per swimmer per day. Smallville has hired you to assess this project. Fortunately, the neighboring identical town of Springfield already has a pool, and the town has randomly varied the price of that pool to find how price affects usage. The results from their study follow:

Price/day Number of swimmers/day
$8 800
$10 400
$4 1,600
$6 1,200

If the swimming pool is built as planned, what would be the net benefit per day from the wimming pool? What is the consumer surplus per day? What is the producer surplus per day?

Answer 1

The answer is "2,400, 3,600, and 2,400".

Step-by-step explanation:

Please find the complete question in the attached file.

using the table to calculate the linear demand function.

Function Linear Demand:
`P = a - bQ`

`Q = 2,000\\\\P = 2 \\\\Q = 400\\\\P = 10`

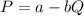
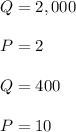
`2 = a - 2,000b.........(1)\\\\10 = a - 400b..........(2) \\\\\ subtract \ equation \ (2) \ from \ (1):\\\\1,600b = 8\\\\b=(8)/(1600)\\\\ b = 0.005\\\\ a = 10 + 400b [From \ equation \ (2)] = 10 + 400 x 0.005 = 10 + 2 = 12\\\\Demand \ function( P) = 12 - 0.005Q`

In point (i)

`P = 6\\\\6 = 12 - 0.005Q\\\\ 0.005Q = 6\\\\Q = 1200\\\\\to Net\ benefit\ = Q * (P - MC) \\\\`

`= 1200 * (6 - 4)\\\\ = 1200 * 2\\\\ = \$2,400`

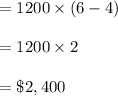
In point (ii)

If Q = 0, P = 12 (vertical intercept of demand curve)

Cost surplus = surface area

`=((1)/(2)) * (12 - 6) * 1200 \\\\ = 600 * 6 \\\\ =\$3,600`

In point (iii)

Surplus for producer = region of MC curve and price

`= (6 - 4) * 1200 \\\\ = 1200 * 2 \\\\= \$2,400`