Question

Assume that the helium porosity (in percentage) of coal samples taken from any particular seam is normally distributed with true standard deviation 0.78.

(a) Compute a 95% CI for the true average porosity of a certain seam if the average porosity for 15 specimens from the seam was 4.85. (Round your answers to two decimal places.)
(b) Compute a 98% CI for true average porosity of another seam based on 11 specimens with a sample average porosity of 4.56. (Round your answers to two decimal places.)
(c) How large a sample size is necessary if the width of the 95% interval is to be 0.46? (Round your answer up to the nearest whole number.)
(d) What sample size is necessary to estimate true average porosity to within 0.18 with 99% confidence? (Round your answer up to the nearest whole number.)

Answer 1

a) The 95% CI for the true average porosity of a certain seam if the average porosity for 15 specimens from the seam was 4.85 is (4.46, 5.24).

b) The 98% CI for true average porosity of another seam based on 11 specimens with a sample average porosity of 4.56 is (4.01, 5.11).

c) A sample size of 12 is needed.

d) A sample size of 125 is needed.

Explanation:

(a) Compute a 95% CI for the true average porosity of a certain seam if the average porosity for 15 specimens from the seam was 4.85.

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.95)/(2) = 0.025`

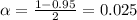
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
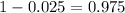`1 - 0.025 = 0.975`, so Z = 1.96.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

`M = 1.96(0.78)/(√(15)) = 0.39`

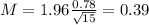
The lower end of the interval is the sample mean subtracted by M. So it is 4.85 - 0.39 = 4.46

The upper end of the interval is the sample mean added to M. So it is 4.85 + 0.39 = 5.24

The 95% CI for the true average porosity of a certain seam if the average porosity for 15 specimens from the seam was 4.85 is (4.46, 5.24).

(b) Compute a 98% CI for true average porosity of another seam based on 11 specimens with a sample average porosity of 4.56. (Round your answers to two decimal places.)

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.98)/(2) = 0.01`

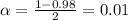
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
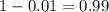`1 - 0.01 = 0.99`, so Z = 2.327.

Now, find the margin of error M as such

`M = z(\sigma)/(√(n))`

In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

`M = 2.327(0.78)/(√(11)) = 0.55`

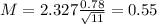
The lower end of the interval is the sample mean subtracted by M. So it is 4.56 - 0.55 = 4.01

The upper end of the interval is the sample mean added to M. So it is 4.56 + 0.55 = 5.11

The 98% CI for true average porosity of another seam based on 11 specimens with a sample average porosity of 4.56 is (4.01, 5.11).

(c) How large a sample size is necessary if the width of the 95% interval is to be 0.46?

95% CI means that
`z = 1.96`

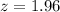
A sample of n is needed, and n is found when M = 0.46. So

`M = z(\sigma)/(√(n))`

`0.46 = 1.96(0.78)/(√(n))`

`0.46√(n) = 1.96*0.78`

`(√(n))^2 = ((1.96*0.78)/(0.46))^2`

`n = 11.05`

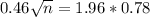
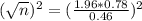
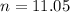
Rounding up

A sample size of 12 is needed.

(d) What sample size is necessary to estimate true average porosity to within 0.18 with 99% confidence?

99% CI means that
`z = 2.575`

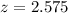
A sample of n is needed, and n is found when M = 0.18. So

`M = z(\sigma)/(√(n))`

`0.18 = 2.575(0.78)/(√(n))`

`0.18√(n) = 2.575*0.78`

`(√(n))^2 = ((2.575*0.78)/(0.18))^2`

`n = 124.5`

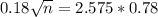
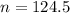
Rounding up

A sample size of 125 is needed.