Answer:
El perímetro del triángulo rectángulo es aproximadamente 29.627.
Explanation:
Las coordendas de los vértices del triángulo rectángulo son
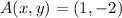 ,
,
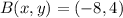 y
y
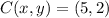 . En primer lugar, determinamos las longitudes de los segmentos AB, BC y AC por el Teorema de Pitágoras:
. En primer lugar, determinamos las longitudes de los segmentos AB, BC y AC por el Teorema de Pitágoras:
![AB = \sqrt{(-8-1)^(2)+[4-(-2)]^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/qw5cybc8l335wk8nt1az18rhbeshz9uv9s.png)
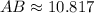
![BC = \sqrt{[5-(-8)]^(2)+(2-4)^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/9bi5ufvenzix4mn0gd7mfkugyhtxe64syz.png)
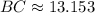
![AC =\sqrt{(5-1)^(2)+[2-(-2)]^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/sxkueypw5i3kd74ed1gtqynb03eqinntnd.png)
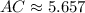
El perímetro del triángulo (
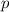 ) es la suma de todos estos segmentos:
) es la suma de todos estos segmentos:
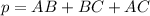
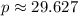
El perímetro del triángulo rectángulo es aproximadamente 29.627.