Question

Ten Points

Look at the rectangle and the square:

A rectangle PQRS and square LMNO are drawn side by side. The length SR of the rectangle is labeled as 12 inches, and the width QR is labeled as 6 inches. The side LM of the square is labeled as 6 inches
Sam says that the length of diagonal SQ is two times the length of diagonal OM.

Is Sam correct? Justify your answer and show all your work. Your work should state the theorem you used to find the lengths of the diagonals.

Answer 1

False

Explanation:

Let's consider the triangle SQR. We know it is right-angle because part of the rectangle PQRS. We can use the Pythagorean theorem:

`SQ^(2) = RQ^(2) + SR^(2) \\SQ^(2) = 36 + 144 = 180\\SQ = √(180) = 13,4`

We can do the same for the square in which ON = 6 because it's a square:

`OM^(2) = MN^(2) + ON^(2) \\OM^(2) = 36 + 36 = 72\\OM = √(72) = 8.5`

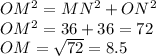
Now let's compare them:

8.5 X 2 = 17 so OM X 2 is not equal to SQ

The sentence is false.

PS : Sorry for the misspelling, I'm French =)