Question

A lumber company is making doors that are 2058.0 millimeters tall. If the doors are too long they must be trimmed, and if the doors are too short they cannot be used. A sample of 25 is made, and it is found that they have a mean of 2043.0 millimeters with a standard deviation of 6.0. A level of significance of 0.1 will be used to determine if the doors are either too long or too short. Assume the population distribution is approximately normal. Is there sufficient evidence to support the claim that the doors are either too long or too short

Answer 1

Due to the test statistic, there is sufficient evidence to support the claim that the doors are too short.

Explanation:

The null hypothesis is:

`H_(0) = 2058`

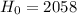
The alternate hypotesis is:

Since the sample mean is less than the expected mean, we test the

`H_(1) < 2058`

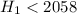
Our test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

A lumber company is making doors that are 2058.0 millimeters tall.

This means that
`\mu = 2058`

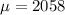
A sample of 25 is made, and it is found that they have a mean of 2043.0 millimeters with a standard deviation of 6.0.

This means, respectively, that
`n = 25, \mu = 2043, \sigma = 6`

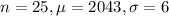
Test statistic:

`z = (2043 - 2058)/((6)/(√(25)))`

`z = -12.5`

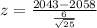
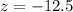
Looking at the z-table, z = -12.5 has a pvalue of 0 < 0.1, which means that there is sufficient evidence to support the claim that the doors are too short.