Question

In 2009 a survey of Internet usage found that 79 percent of adults age 18 years and older in the United States use the Internet. A broadband company believes that the percent is greater now than it was in 2009 and will conduct a survey. The company plans to construct a 98 percent confidence interval to estimate the current percent and wants the margin of error to be no more than 2.5 percentage points. Assuming that at least 79 percent of adults use the Internet, which of the following should be used to find the sample size (n) needed?

a. 1.96 â0.5/n = 0.025
b. 1.96 â0.5(0.5)/n = 0.25
c. 2.33 â0.5(0.5)/n =0.05
d. 2.33 â0.79(0.21)/n= 0.025

Answer 1

`0.025 = 2.33\sqrt{(0.79*0.21)/(n)}`

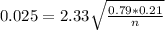
Option d.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

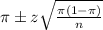
In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

The margin of error is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

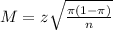
79 percent of adults age 18 years and older in the United States use the Internet.

This means that
`\pi = 0.79`

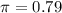
98% confidence level

So
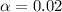`\alpha = 0.02`, z is the value of Z that has a pvalue of
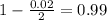`1 - (0.02)/(2) = 0.99`, so
`Z = 2.33`.

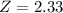Which of the following should be used to find the sample size (n) needed?

We have to find n for which
`M = 0.025`

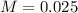
So the equation is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.025 = 2.33\sqrt{(0.79*0.21)/(n)}`

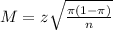
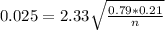
Option d.