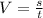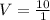Answer:
(a)
i)
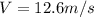
ii)
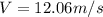
iii)
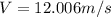
(b)

Explanation:
Given
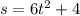
Solving (a): Average velocity between t = 1 and t = 1 + h
When t = 1
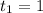
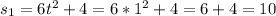
i) h = 0.1
When t = 1 + h
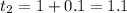
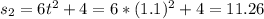
Average velocity is then calculated as:
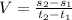
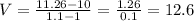
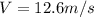
ii) h = 0.01
When t = 1 + h

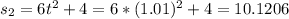
Average velocity is then calculated as:
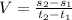
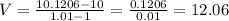
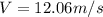
ii) h = 0.001
When t = 1 + h
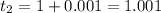
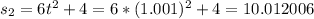
Average velocity is then calculated as:
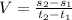
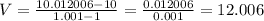
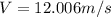
Solving (b): Instantaneous velocity at t = 1
When t = 1


Velocity is: