Question

One end of an elastic cord is fastened to a steel beam. A metal weight with a mass of 68 kg is attached to the other end of the cord and dropped from the level of the beam. The weight is traveling at 14 m/s downward when the rest length of the cord is exceeded and the cord begins to stretch and exert an upward force on the metal weight. After 0. 85 seconds, the weight is moving upward with a speed of 11 m/s. What is the average force on the weight during this time period?.

Answer 1

Hi there!

We can use IMPULSE to solve.

Recall impulse:

`I = \Delta p = m\Delta v = m(v_f - v_i)`

Begin by calculating the impulse. Assuming up to be the + direction, and down to be the - direction.

`I = 68(11 - (-14)) = 68 \cdot 25 = 1700 kg(m)/(s)`

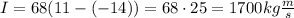
Now, we can calculate force using this value:

`I = F \cdot t\\\\F = (I)/(t)\\\\F = (1700)/(0.85) = \boxed{2000 N}`

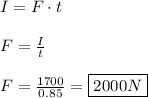
The weight experiences a net force of 2000N UPWARDS.