Question

Suppose that a list contains integers that are in order of largest to smallest and an integer can appear repeatedly in this list.

1) Devise an algorithm that locates all occurrences of an integer x in the list.
2) Estimate the number of comparisons used.
You must show/explain your work.

Answer 1

(a) The algorithm is as follows:

count = 0

for i = 1 to n:

if x = xi:

count++

print(count)

(b) n comparisons

Step-by-step explanation:

Solving (a):

Assume the integer to locate is x and the elements of the list are:
`x_1, x_2, x_3, x_4..... x_n`

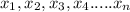
Such that:
`x_1 \ge x_2 \ge x_3 ...... \ge x_n`

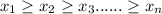
The algorithm is as follows:

count = 0

for i = 1 to n:

if x = xi:

count++

print(count)

The above iterates through the count of the list (i.e. n) and makes comparison with each element of the list (i.e. element 1 to element n).

When a match is found, the count variable is incremented by 1 and printed at the end of the loop

Furthermore:

If there are 3 elements in the list, the algorithm makes 3 comparisons.

It makes 10 comparisons if there are 10 elements in the list.

So: it makes n elements if there are n elements in the list